M24 Statistik 1:  Wintersemester 23/24

Vorlesung 13: Metaanalyse

 

Prof. Matthias Guggenmos

Health and Medical University Potsdam

Der Forschungsprozess

Beispiel

Wir interessieren uns für den Zusammenhang zwischen der Nutzung sozialer Medien und psychischer Gesundheit.

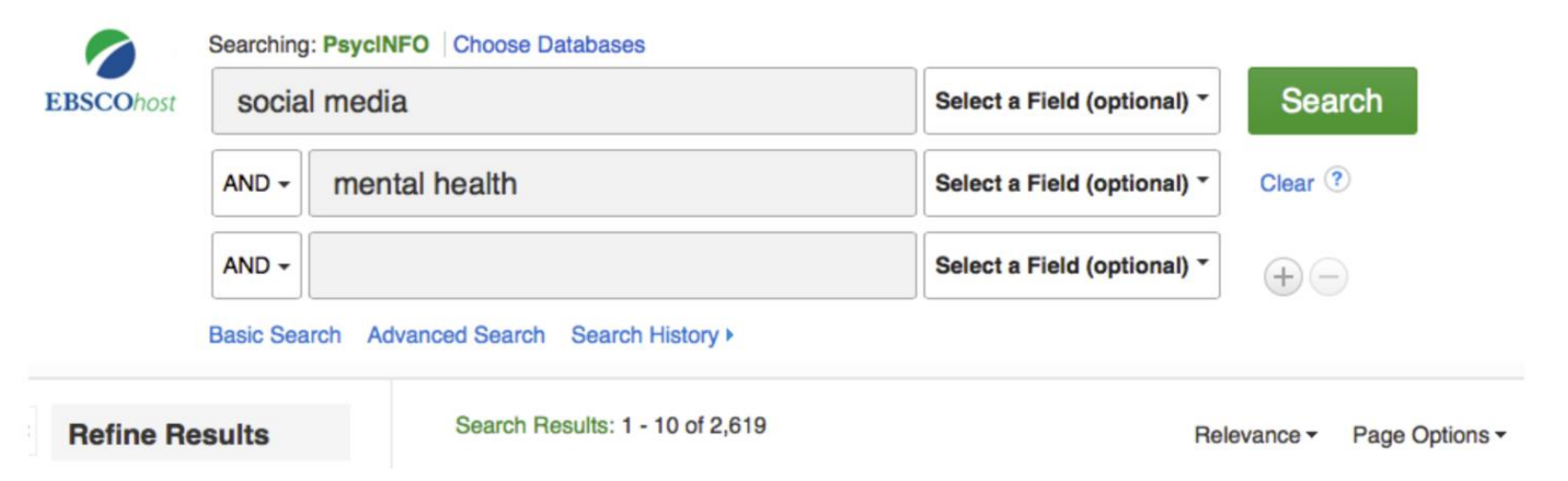
→ Für Details zur Literatursuche, siehe Vorlesung Forschungsmethoden.

Beispiel

Ein hypothetischer Beispielartikel aus der Literatursuche:

• Frage: wie kombinieren wir die Effekte vieler solcher Studien?

Metaanalyse – die Königsdisziplin

Bildnachweis¹

• Aber beachte: die Qualität von Reviews und Metaanalysen hängt von der Qualität der einzelnen Studien ab! So kann etwa eine große Metaanalyse auf Basis von verzerrten Studien eine geringere Evidenzqualität haben, als ein einzelner RCT (randomized controlled trial).

Was ist eine Metaanalyse?

• Generelle Idee: viele Studien sagen mehr als eine Einzelne

	Eine Metaanalyse kombiniert die berichteten Effekte verschiedener Studien mit dem Ziel eine genauere Schätzung eines Effektes zu berechnen.

• Eine Metaanalyse kann auf unstandardisierten oder standardisierten Effekten basieren.
• Unstandardisierte Effekte:
  • Relative/absolute Häufigkeiten
  • Lagemaße
  • Streuungsmaße
  • Unterschiede
  • Kovarianz, Regressionskoeffizient
• Standardisierte Effekte (aka Effektstärke):
  • Cohen’s d
  • Korrelation
    

xkcd #2755²

Geschichte der Metaanalyse

• Stammt aus der Psychologischen Forschung
• Erste Metaanalyse von Hans Jürgen Eysenck (1952): Wirksamkeit der Psychoanalyse und anderer Therapieformen
• Begriff “Metaanalyse” eingeführt von Gene Glass:

“Meta-analysis refers to the analysis of analyses. I use it to refer to the statistical analysis of a large collection of analysis results from individual studies for the purpose of integrating the findings. It connotes a rigorous alternative to the casual narrative discussions of research studies which typify our attempts to make sense of the rapidly expanding research literature.”

Glass (1976)³

Hans Jürgen Eysenck

Gene Glass

Vorgehen bei einer Metaanalyse

Für eine konkrete Fragestellung:

1. Nach relevanten Forschungsarbeiten suchen (Datenbanken, Google, Bibliothek, Referenzen in Forschungsarbeiten…)
2. Ein- und Ausschlusskriterien festlegen (z.B. Randomisierung, Kontrollgruppen, Ausschluss von Alternativerklärungen…)
3. Auswahl relevanter Studien: Ein- und Ausschlusskriterien, genaue Fragestellung (dieselbe abhängige Variable?)
4. Sich auf einen Kennwert einigen (z.B. \(r\))
5. Für alle Studien die Ergebnisse in diesen Kennwert umrechnen, falls sie nicht schon so vorliegen
6. Kennwerte mitteln (i.d.R. an der Stichprobengröße/Varianz gewichteter Mittelwert)

Bildnachweis⁴

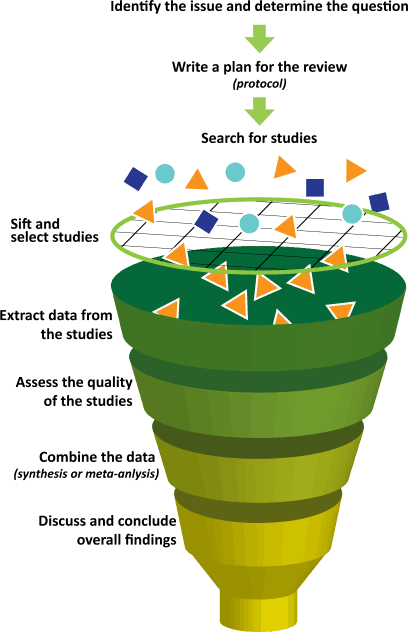
Vorgehen bei einer Metaanalyse

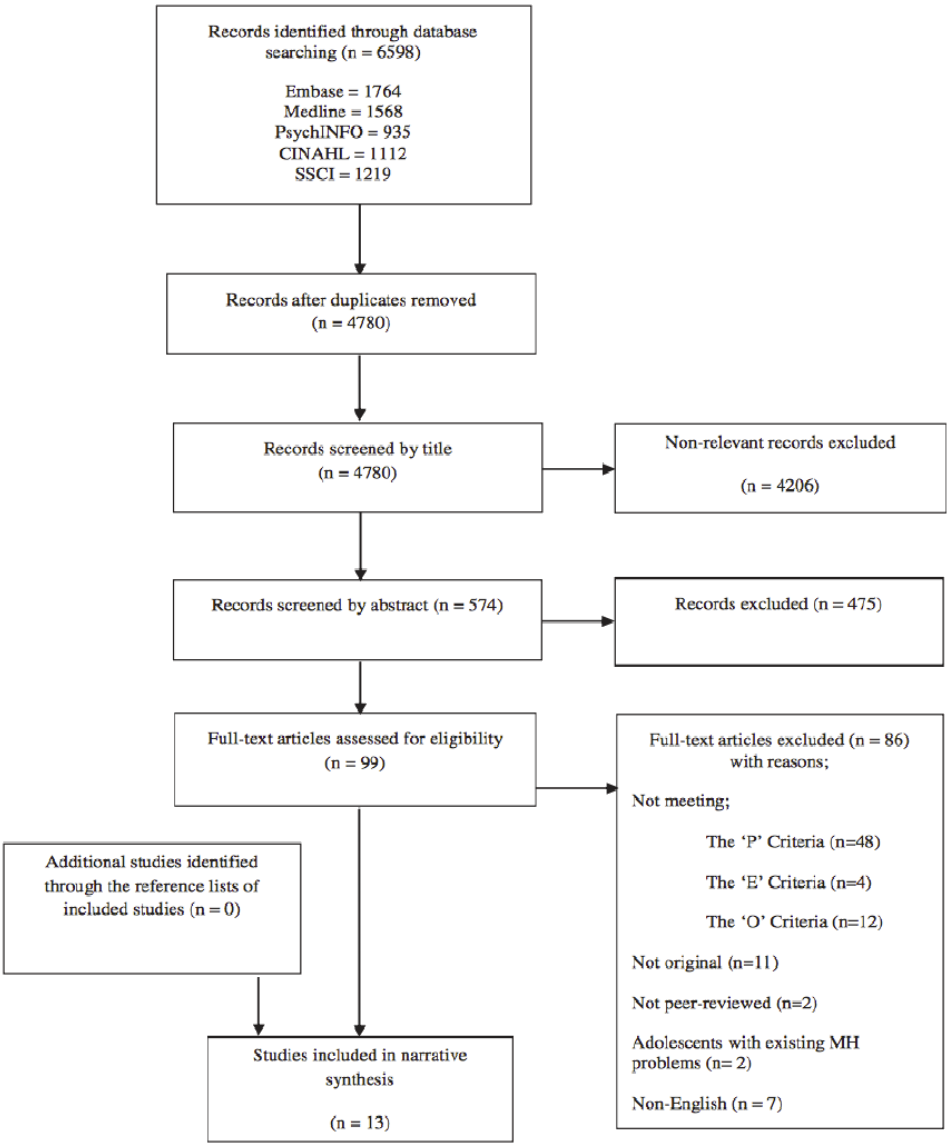
Die Suche und Auswahl der relevanten Studien sowie die Effekte der Ein- und Ausschlusskriterien werden in einem Flussdiagramm dargestellt.

Im Beispielflusdiagramm wird das PEO-Framework zur Auswahl relevanter Studien benutzt:

• Population (‘P’ Criteria)
  Welche Population wird untersucht? Frauen, Studierende, Menschen mit spezifischer Diagnose, …
• Exposure (‘E’ Criteria) — die unabhängige Variable
  Welche Erkrankung weist die Population auf ODER welchem potentiellen Risikofaktor war die Population ausgesetzt ODER welcher Intervention / Treatment wurde die Population unterzogen?
• Outcome (‘O’ criteria) — die abhängige Variable
  Was wird gemessen? Wahrscheinlichkeit einer Erkrankung, Heilungsfortschritt, Lebensqualität, Einstellungen, usw.

Vorgehen bei einer Metaanalyse

Beispiel am Mittelwert: die Mittelwerte verschiedener Studien bilden selbst wieder eine Verteilung — die empirische Stichprobenverteilung.

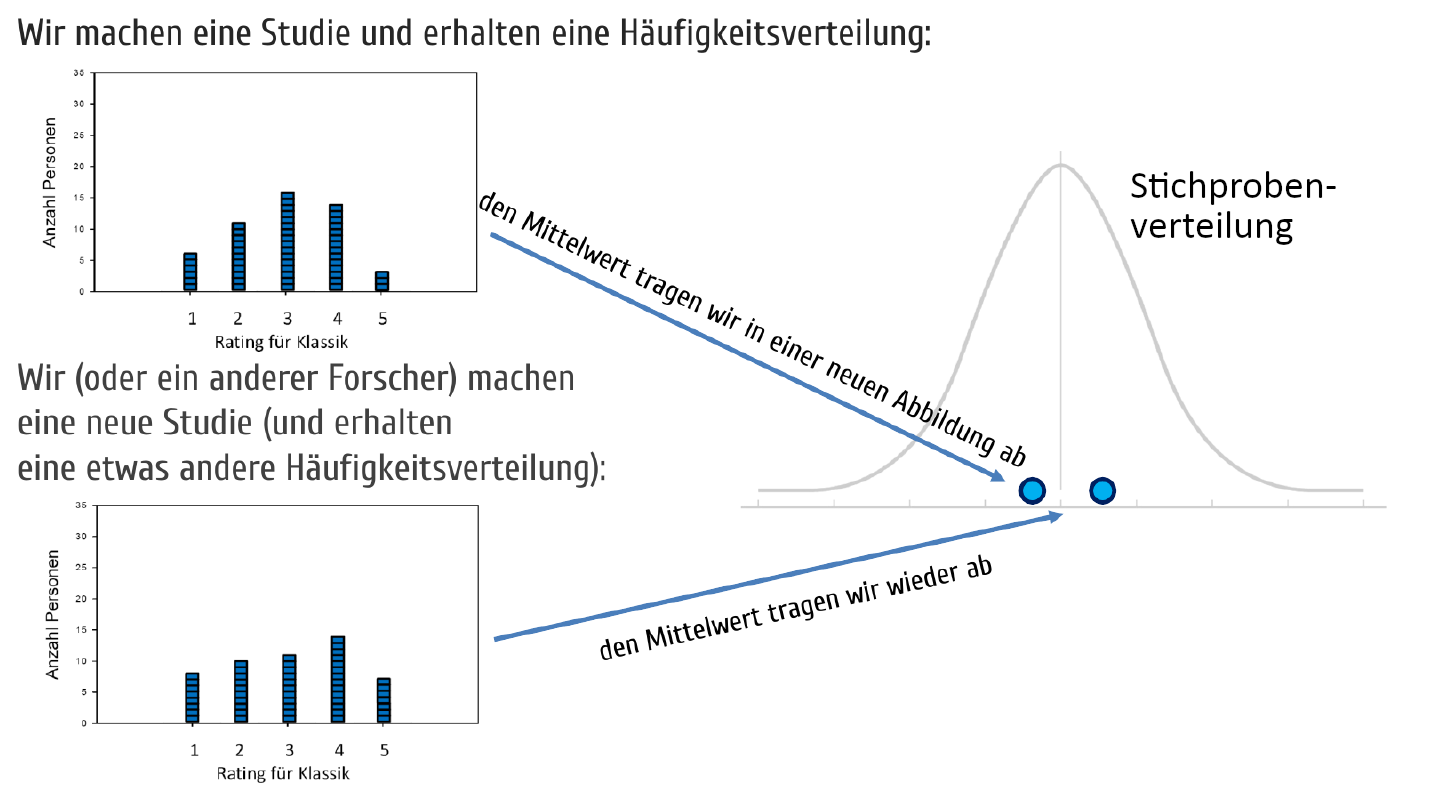
Vorgehen bei einer Metaanalyse

Beispiel am Mittelwert: die Mittelwerte verschiedener Studien bilden selbst wieder eine Verteilung — die empirische Stichprobenverteilung.

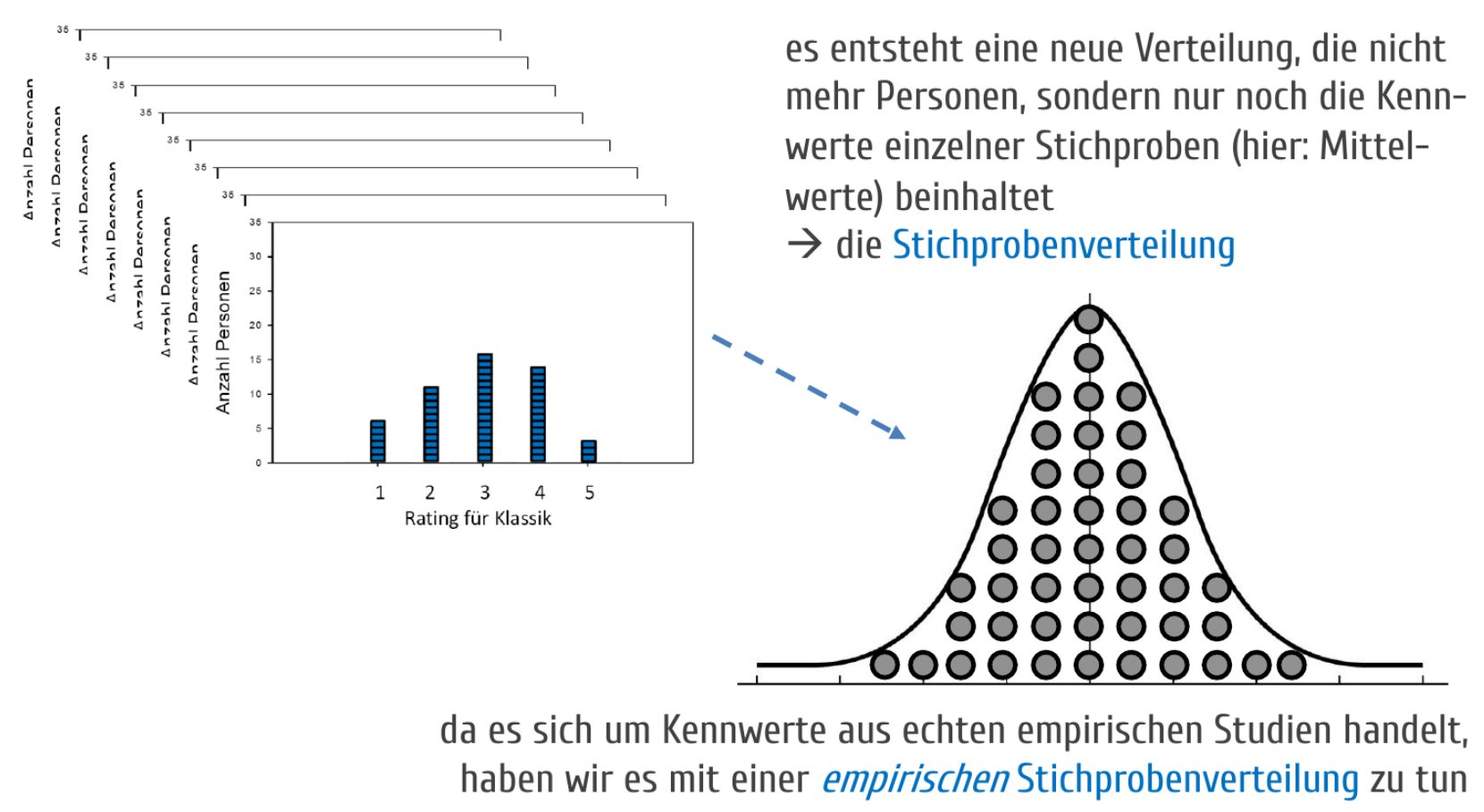
Berechnung eines metaanalytischen Mittelwertes

• Hauptergebnis einer Metaanalyse ist ein gemittelter statistischer Kennwert für das untersuchte Phänomen.
• Ein häufiger Ansatz ist dabei, nicht die unstandardisierten Effekte (z.B. \(\bar{x}\) oder \(b_1\)) selbst zu mitteln, sondern die entsprechenden standardisierten Effektstärken (z.B. Cohen’s \(d\) oder \(r\)).
  • Reminder: standardisierte Effekte sind besser vergleichbar zwischen Studien!
• In der Regel wird bei der Mittelwertbildung ein gewichteter Mittelwert verwendet, damit verlässlichere Studien stärker einfließen.
• Gewichtungsformel für Cohen’s \(d\) für i=1..n Studien:

\[ \bar{d} = \frac{d_1w_1+d_2w_2+...}{\sum w_i} = \frac{\sum d_i w_i}{\sum w_i} \]

• \(\bar{d}\) ist die Schätzung der (mittleren) Effektstärke auf Basis aller Studien.
• Die Gewichtungsfaktoren \(w_i\) hängen in erster Line von der Stichprobengröße ab – je größer die Stichprobe, desto größer \(w_i\), desto mehr fließt die Studie in den Mittelwert ein.

Gewichtungsfaktor bei Cohen’s d

• Die Gewichtungsfaktoren berechnen sich je nach Kenngröße verschieden.
• Die gängigste Methode ist die Gewichtung an der inversen Samplingvarianz:

\[ w_i = \frac{1}{v_i} \]

• Die Samplingvarianz gibt die Varianz der Kennwerte an, die man bei wiederholter Durchführung der identischen Studie erhalten würde.
  • Beachte: Samplingvarianz ≠ Stichprobenvarianz/Samplevarianz!
• Dank des zentralen Grenzwertsatzes kann diese diese Varianz ohne tatsächliche Wiederholungen der Studie geschätzt werden.
  • Reminder: wird ein statistischer Kennwert in mehreren Stichproben aus derselben Population bestimmt, folgen die Kennwerte asymptotisch einer Normalverteilung (d.h. für Anzahl Stichproben \(\rightarrow\infty\))
    
  • Diese Logik der Stichprobenverteilung ist bereits bekannt Standardfehler bekannt — tatsächlich ist die Samplingvarianz einfach der Standardfehler zum Quadrat: \(v_i = \hat{se}^2\)
• Die Samplingvarianz hängt stark von der Stichprobenzahl der Studien ab — je höher,
  desto (erwartbar) weniger werden wiederholt mit dieser Stichprobenzahl
  bestimmter Kennwerte schwanken, desto kleiner also die Samplingvarianz.

Inverse Samplingvarianz: Formeln

• Cohen’s d (unabhängige Messungen Gruppen A und B):

\[ v_i = \frac{n_A + n_B}{n_A n_B} + \frac{d^2}{2(n_A+n_C)} \]

\(n_A\)/\(n_B\) sind die Fallzahlen in den Gruppen A/B der Studie \(i\), \(d\) ist das Cohen’s \(d\) der Studie.

• Cohen’s d (abhängige Messungen) ^{5 6}:

\[ v_i = \frac{d^2+2}{2n} \]

• Pearson-Korrelation (Annahme: z-transformierte Korrelationskoeffizienten — häufigster Fall!):

\[ v_i = \frac{1}{n-3} \]

• Pearson-Korrelation (Rohe Korrelationskoeffizienten):

\[ v_i = \frac{\left(1-r^2\right)^2}{n-1} \]

Ergebnis der Metaanalyse

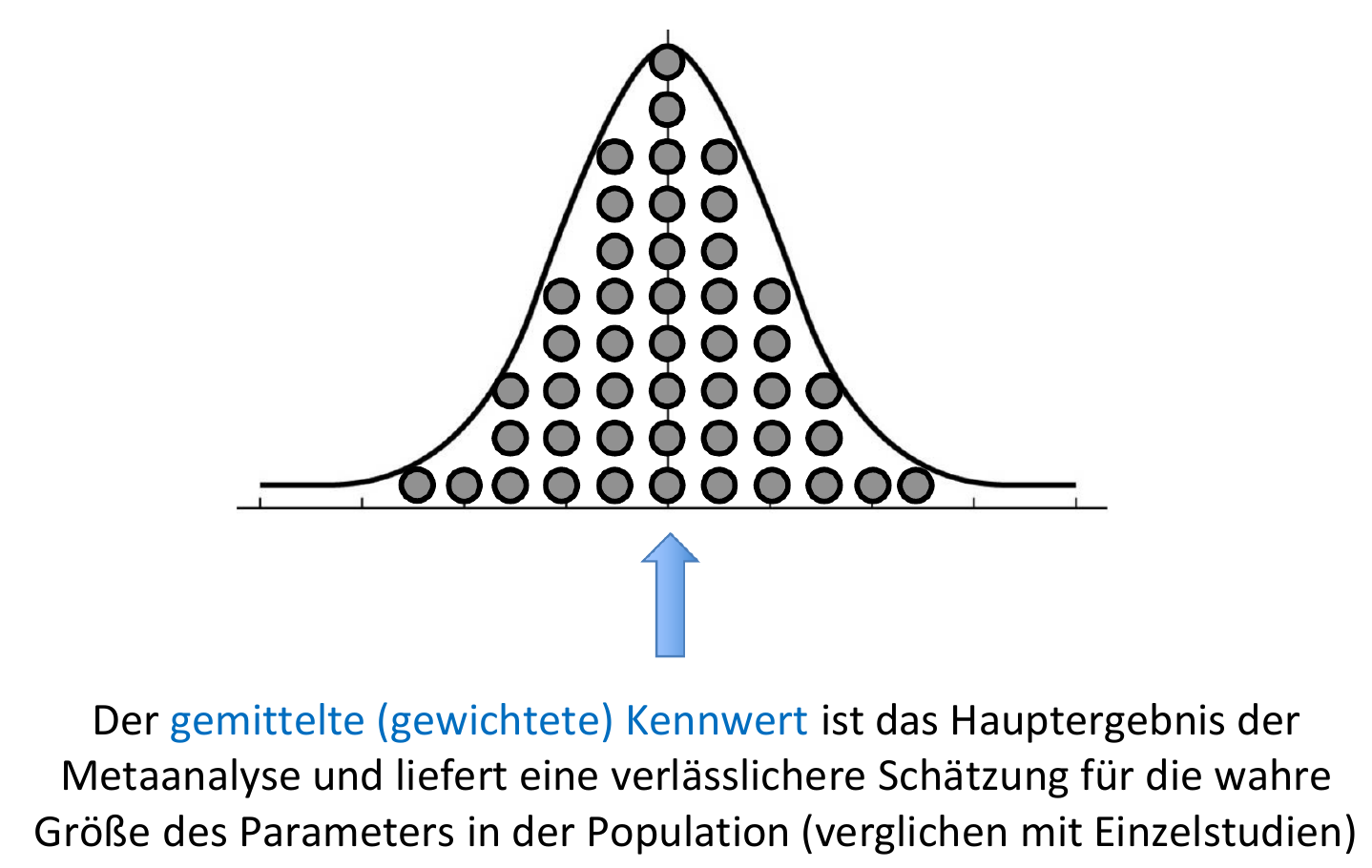
Beispiel 1: wirkt Psychotherapie?

• Metaanalyse von Smith und Glass (1977)⁷
• Verglichen wurde „Therapie vs. keine Therapie” für eine Reihe von psychischen Störungen (knapp 400 Studien insgesamt):
• Berechnet wurde schließlich ein mittleres d:

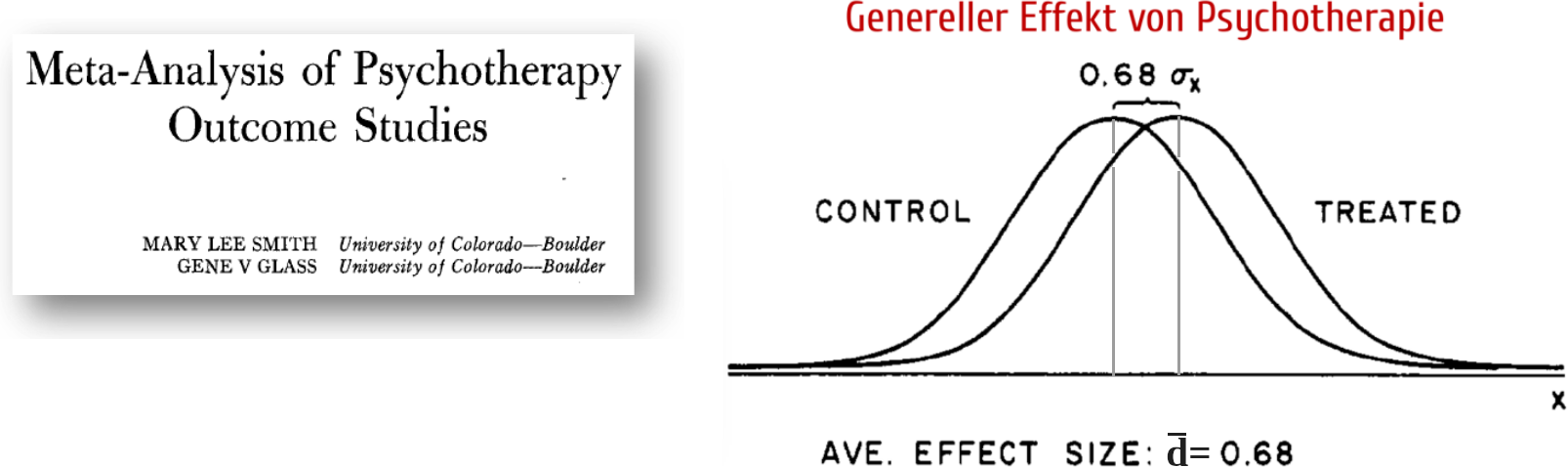
Beispiel 1: wirkt Psychotherapie?

• Metaanalyse von Smith und Glass (1977)⁸
• Moderatorvariable 1: unterscheidet sich die Wirksamkeit je nach Art der Therapie?

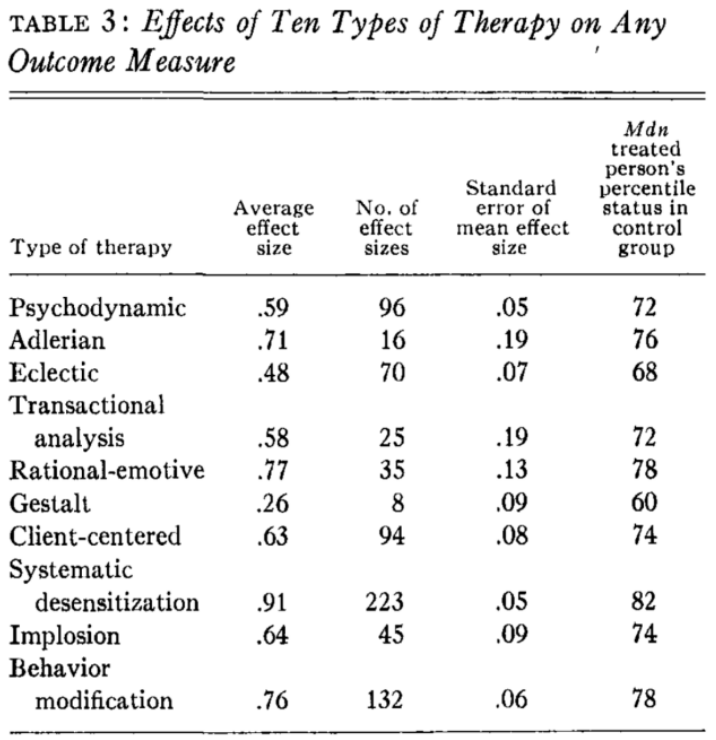
Nach dieser Metaanalyse weisen die unterschiedlichen Psychpotherapie-Schulen/Arten deutlich unterschiedliche Effektstärken auf: Spannbreite von Gestalttherapie \((d=0{,}26)\) bis Systematische Desensibilisierung (Expositionstherapie) \((d=0{,}91)\)

Ergebnis ist mit Vorsicht zu genießen: keine Information über die jeweils behandelten Erkrankungen; recht alte Studie, die Probleme wie Publikationsbias und Studienqualität nicht nach heutigen Maßstäben berücksichtigt.

Beispiel 1: wirkt Psychotherapie?

• Metaanalyse von Smith und Glass (1977)⁹
• Moderatorvariable 2: unterscheidet sich die Wirksamkeit je nach Outcome-Maß?

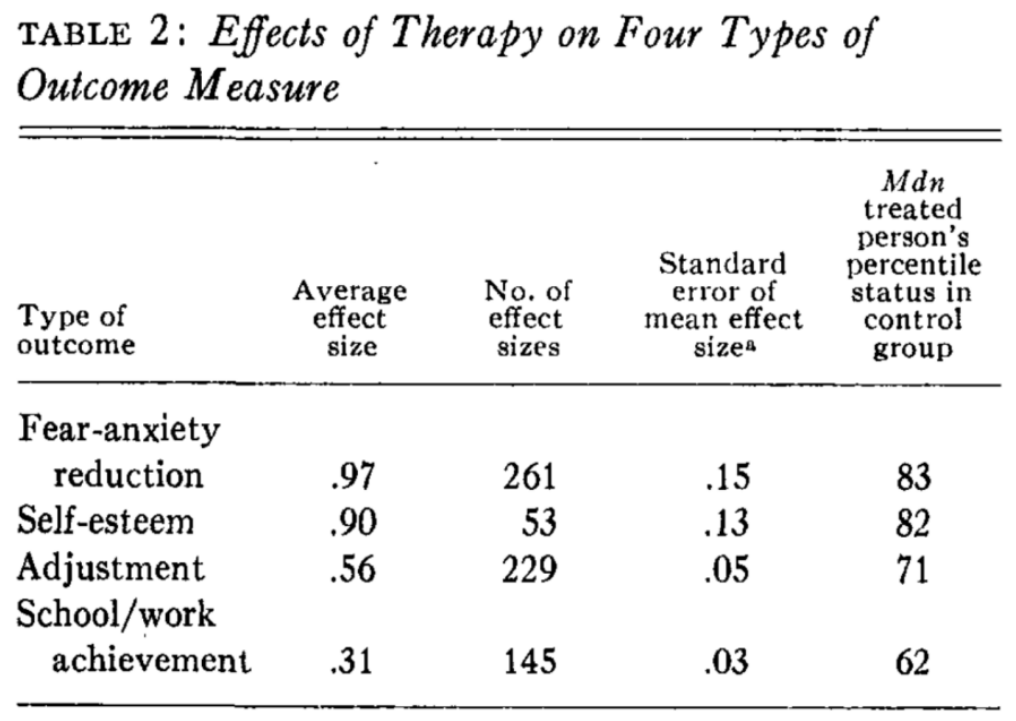
Recht große Verbesserung auf der Angstachse \((d=0{,}97)\), eher geringe Verbesserung im Schul/Arbeitsumfeld \((d=0,{31})\).

Ergebnis ist mit Vorsicht zu genießen: keine Information über die jeweils behandelten Erkrankungen; recht alte Studie, die Probleme wie Publikationsbias und Studienqualität nicht nach heutigen Maßstäben berücksichtigt.

Beispiel 1: wirkt Psychotherapie?

• Metaanalyse von Smith und Glass (1977)¹⁰
• Unterschiede zwischen Verhaltenstherapie (behavioral) und anderen Therapieformen (nonbehavioral)

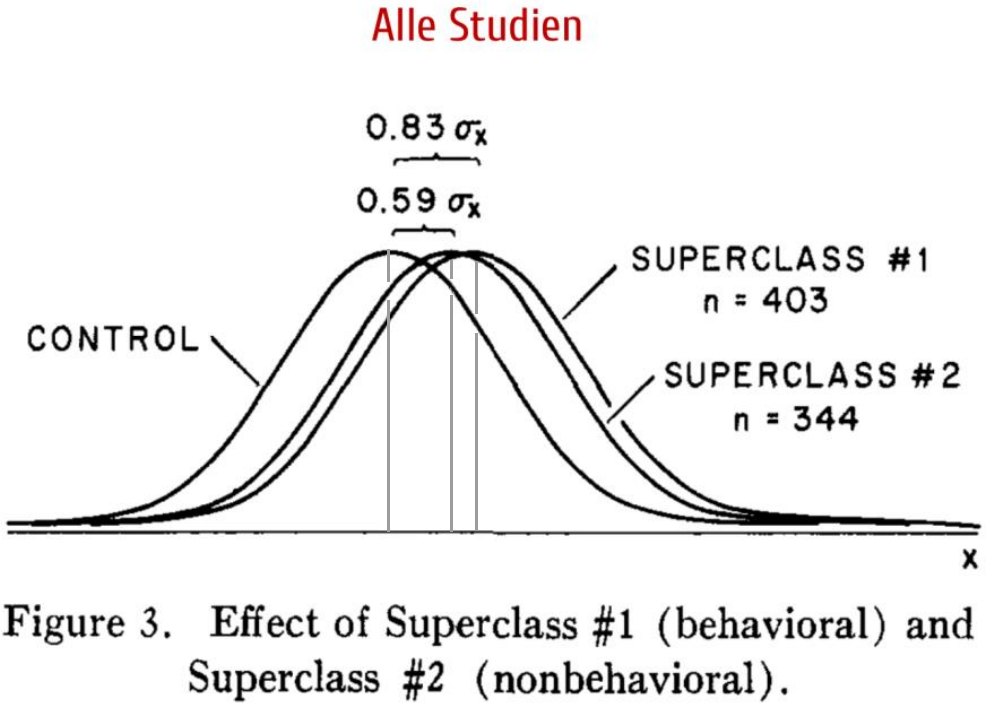
Für diese Analyse wurden die verschiedenen Therapieformen in die Superklassen “behavioral” (403 Studien) und “nonbehavioral” (344 Studien) unterteilt. Die Analyse zeigt einen Vorteil für Verhaltenstherapie an (\(d=0{,}83\) vs. \(d=0{,}59\)).

Ergebnis ist mit Vorsicht zu genießen: keine Information über die jeweils behandelten Erkrankungen; recht alte Studie, die Probleme wie Publikationsbias und Studienqualität nicht nach heutigen Maßstäben berücksichtigt.

Beispiel 2: Musikpräferenzen und Persönlichkeit

• Moderne Metaanalyse von Schäfer & Mehlhorn (2017)¹¹

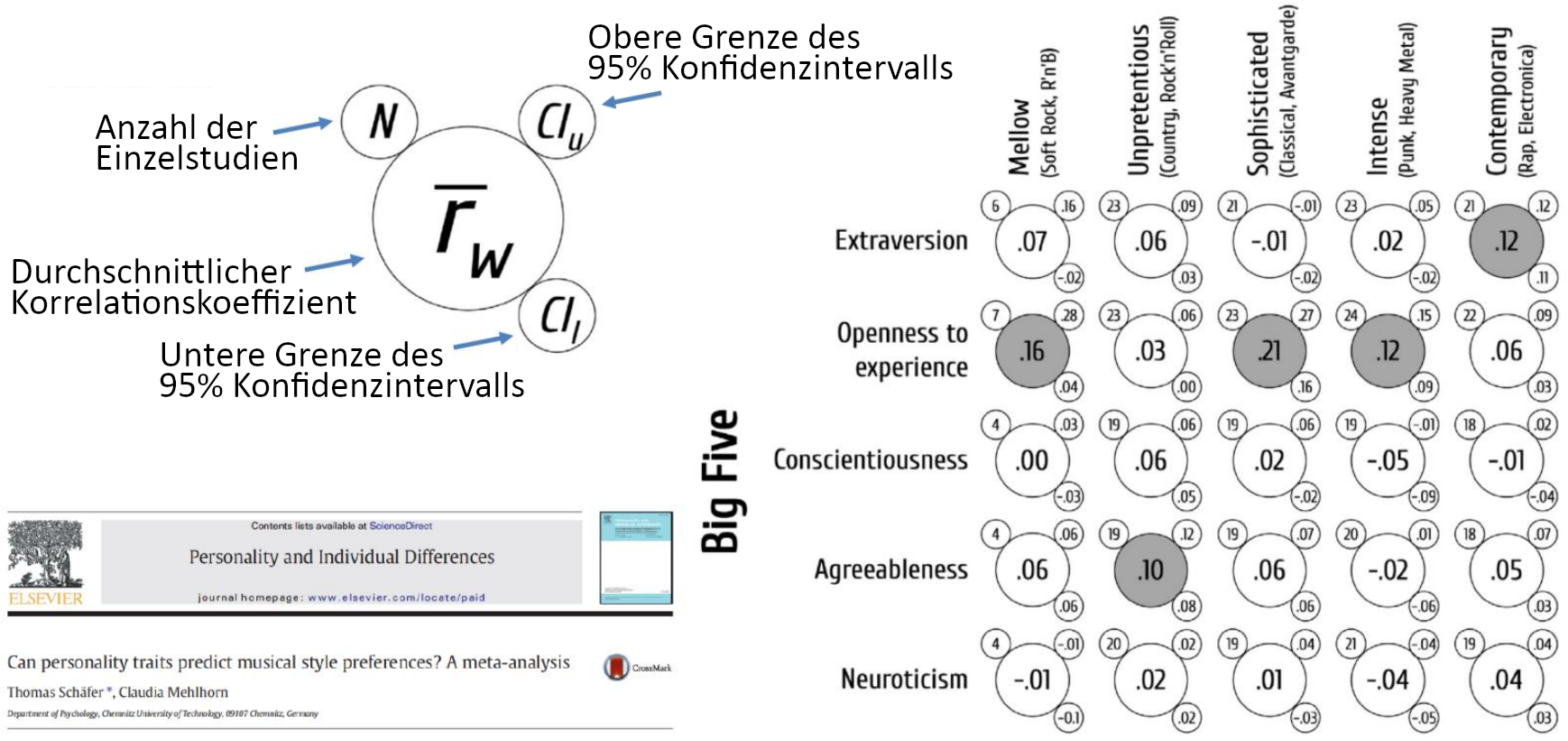
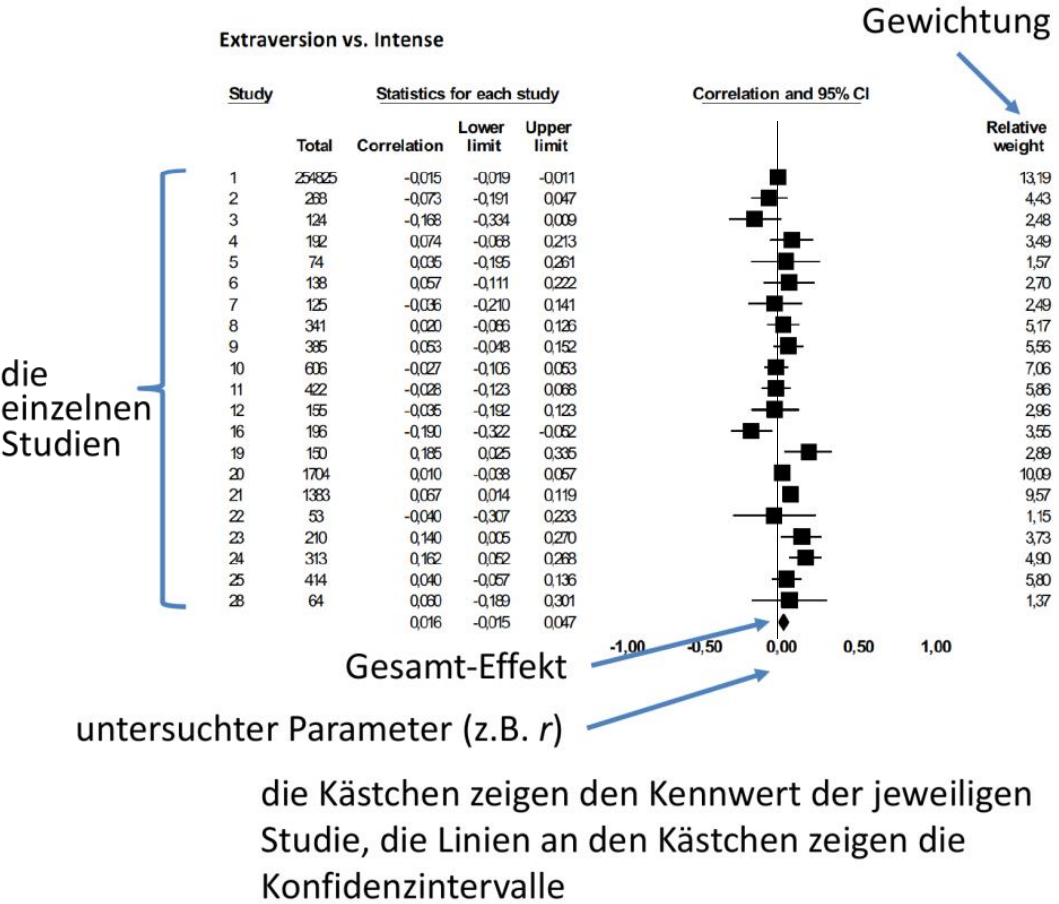
Forest-Plot

Die Ergebnisse der einbezogenen Studien sowie das Gesamtergebnis werden in einem Forest-Plot dargestellt (zeigt die Effekte und ihre Konfidenzintervalle).

• Schnelle visuelle Orientierung über gemeinsame Trends der betrachteten Studien.
• Jedes quadratische Kästchen repräsentiert die Effektstärke einzelner Studien.
• Konfidenzintervalle geben Unsicherheit der einzelnen Studien an.
• Diamant-Symbol in der letzten Reihe zeigt den gemittelten Gesamteffekt.

Probleme bei einer Metaanalyse

Problem 1: Qualität der einfließenden Studien ist nicht zufriedenstellend (in der Praxis ein sehr häufiges Problem) — „garbage-in-garbage-out“.

• Lässt sich prinzipiell durch gut gewählte Ein- und Ausschlusskriterien vermeiden — allerdings bleiben dann oft nur sehr wenige Studien übrig.
• Alternative: methodische Qualität codieren und als Gewichtung einfügen.

Problem 2: die einfließenden Studien messen nicht genau dasselbe Konstrukt — „Äpfel-Birnen-Problem“.

• Unterschiedliche abhängige Variablen (d.h. Outcomes).
• Effekte sind dann nicht oder nur begrenzt vergleichbar.
• Diagnose durch die psychometrische Metaanalyse:
  • Einteilung der Studien in Subgruppen mit jeweils einheitlichen abhängigen Variablen.
  • Ist die Varianz innerhalb der Subgruppen deutlich kleiner als die Varianz aller Studien kombiniert (“wenn alles in einem Topf“ liegt”): Hinweis auf unzulässige Vermischung der abhängigen Variablen.
    ⇒ „Äpfel“ und „Birnen“ sollten dann in getrennten Analysen untersucht werden.

Probleme bei einer Metaanalyse

Problem 3: Mehrere Studienergebnisse pro Artikel – Abhängigkeitsproblem

• Mehrere Effekte, die in einem einzelnen Artikel berichtet werden, sind typischerweise nicht unabhängig (insbesondere Überlapp der Versuchspersonen).
• Lösung: zunächst den mittleren (aggregierten) Effekt pro Artikel bestimmen und diesen in die Metaanalyse aufnehmen.

Problem 4: die einfließenden Studien bilden kein repräsentatives Abbild aller Studien zur Fragestellung — Publikationsbias

• Der gemittelte Effekt als Hauptergebnis ist dann verzerrt und möglicherweise unbrauchbar.
• Diagnose: Funnel Plot, p-curve, p-uniform
• Lösung: im Prinzip keine (es gibt Vorschläge – z. B. trim-and-fill, p-curve, p-uniform – aber diese schneiden in Simulationsstudien unzureichend ab).

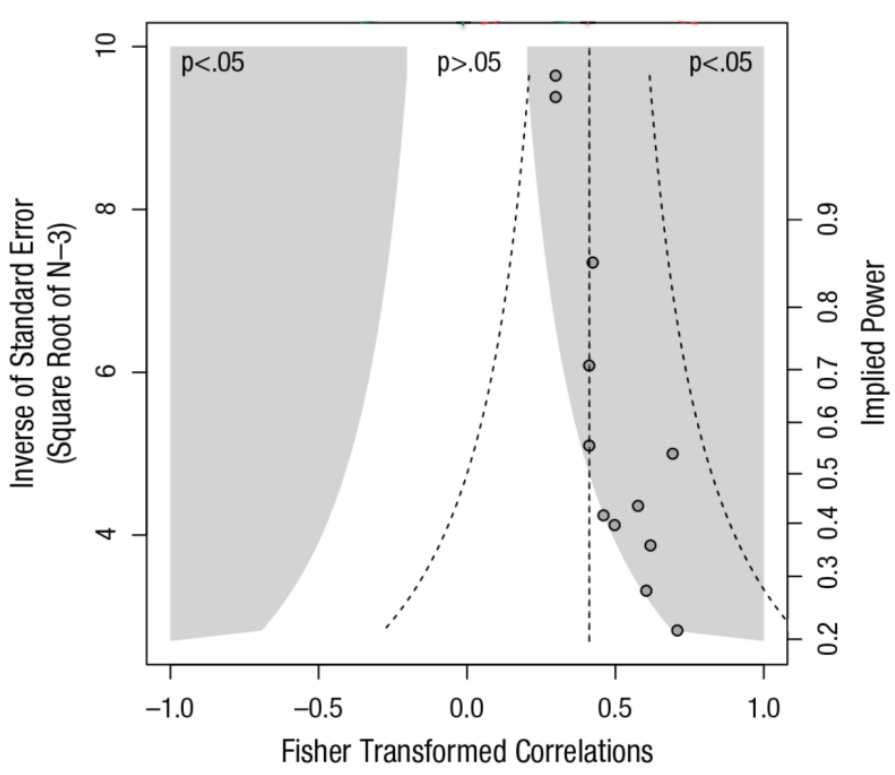
Funnel plot

Funnel Plot: visuelle Methode zur Diagnose eines Publikationsbias’

• Effekte aller Studien werden gegen ihre jeweilige Präzision abgetragen (z. B. Stichprobengröße \(n\)).
• Wenn kein Publikationsbias vorliegt, sollte ein umgekehrter Trichter (engl. funnel) entstehen, da die Varianz der Schätzungen bei größeren Stichproben systematisch kleiner werden sollte (Gesetz der großen Zahl).
• Wenn ein Publikationsbias vorliegt, wird der Funnel asymmetrisch,

Funnel plot

Funnel Plot: visuelle Methode zur Diagnose eines Publikationsbias’

• Beispiel: Meta-Analyse zum Zusammenhang von Habituationsfähigkeit im Kindesalter und späterem IQ¹²

If science were a game, a dominant rule would probably be to collect results that are statistically significant. Several reviews of the psychological literature have shown that around 96% of papers involving the use of null hypothesis significance testing report significant outcomes for their main results but that the typical studies are insufficiently powerful for such a track record. We explain this paradox by showing that the use of several small underpowered samples often represents a more efficient research strategy (in terms of finding p < .05) than does the use of one larger (more powerful) sample.

Bakker et al (2012): The Rules of the Game Called Psychological Science.

• Eine Metaanalyse aggregiert standardisierte oder unstandardisierte Effekte aus verschiedenen Studien.
  • Sie basiert also auf einer empirischen Stichprobenverteilung.
• Die Bestimmung des mittleren Effektes erfolgt in der Regel mit einem gewichteten Mittelwert.
  • Gewichtung anhand der Präzision der einzelnen Studien (die Präzision hängt stark von der Stichprobengröße ab).
• Metaanalysen liefern bessere Schätzungen für den wahren Populationseffekt als einzelne Studien.
• Ergebnisse von Metaanalysen sind häufig durch einen Publikationsbias verzerrt, da vorrangig große/signifikante Effekte publiziert wurden – der wahre Effekt wird dann überschätzt.

xkcd#1477

Fußnoten

1. https://openmd.com/guide/levels-of-evidence

2. https://xkcd.com/2755/

3. Glass, G. V. (1976). Primary, Secondary, and Meta-Analysis of Research. Educational Researcher, 5(10), 3. doi:10.2307/1174772

4. Askie, L., & Offringa, M. (2015). Systematic reviews and meta-analysis. Seminars in Fetal and Neonatal Medicine, 20(6), 403–409. doi:10.1016/j.siny.2015.10.002

5. Borenstein, M. (2009). Effect sizes for continuous data. In H. Cooper, L. V. Hedges & J. C. Valentine (Eds.), The Handbook of Research Synthesis and Meta-Analysis (pp. 221-236). New York: Russell Sage Foundation.

6. https://stats.stackexchange.com/questions/226836/sampling-variance-for-meta-analysis-one-sample-data

7. Smith ML, Glass GV (1977) Meta-analysis of psychotherapy outcome studies. American Psychologist 32:752–760.

8. Smith ML, Glass GV (1977) Meta-analysis of psychotherapy outcome studies. American Psychologist 32:752–760.

9. Smith ML, Glass GV (1977) Meta-analysis of psychotherapy outcome studies. American Psychologist 32:752–760.

10. Smith ML, Glass GV (1977) Meta-analysis of psychotherapy outcome studies. American Psychologist 32:752–760.

11. Schäfer T, Mehlhorn C (2017) Can personality traits predict musical style preferences? A meta-analysis. Personality and Individual Differences 116:265–273.

12. Bakker M, Van Dijk A, Wicherts JM (2012) The Rules of the Game Called Psychological Science. Perspect Psychol Sci 7:543–554.