M24 Statistik 1: Wintersemester 23/24
Vorlesung 03: Lage- und Streuungsmaße
Prof. Matthias Guggenmos
Health and Medical University Potsdam


Die Daten der ersten Beobachtungsstudie zu Paradoxia sind frisch eingetroffen!
| id | group | hours_tiktok_per_day | inflammation |
|---|---|---|---|
| 1 | control | 1.14 | 0.24 |
| 2 | control | 2.24 | 0.19 |
| … | … | … | … |
| 50 | control | 1.14 | 0.13 |
| 51 | paradoxia | 1.57 | 0.03 |
| 52 | paradoxia | 2.59 | 0.21 |
| … | … | … | … |
| 100 | paradoxia | 0.52 | 0.12 |
Hier ist das Histogramm der TikTok-Zeiten von Paradoxikern:
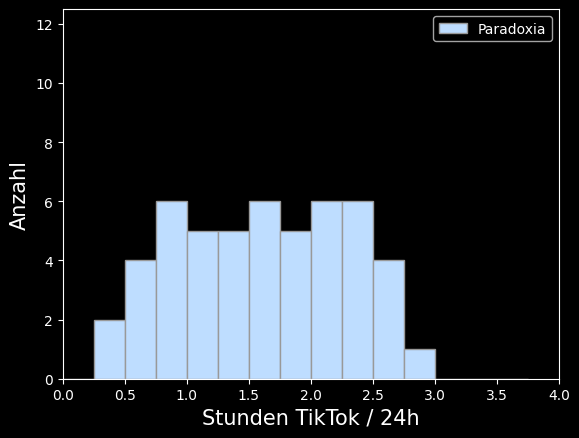
Überschlagen Sie: passt das Histogramm zur angegeben Stichprobe von n=50 Paradoxikern? Und handelt es sich um eine Abbildung relativer oder absoluter Häufigkeit?
Vergleich mit der Kontrollgruppe:
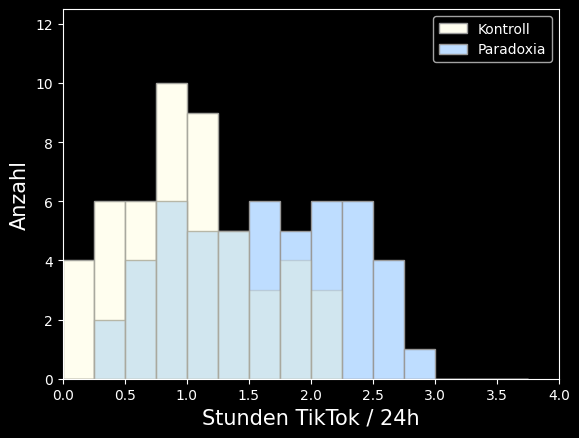
Wir können hier schon erahnen, dass die Studie tatsächlich Evidenz für einen erhöhte TikTok-Zeit bei Paradoxikern erbringt (Hypothese 1)!
Erinnerung: statt der Anzahl (absolute Häufigkeit) kann auch die Wahrscheinlichkeit (relative Häufigkeit) dargestellt werden:
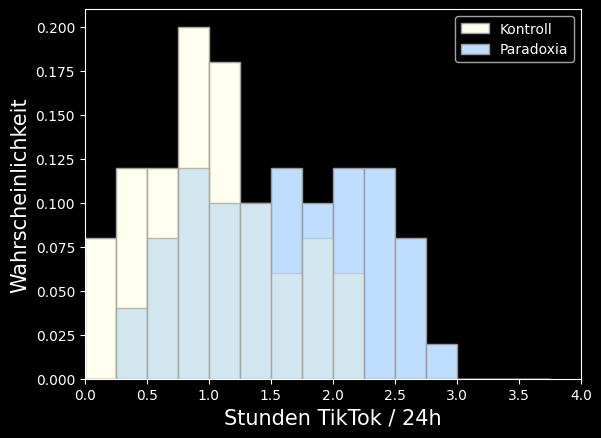
Jeder Wert in dieser Abbildung gibt also die Wahrscheinlichkeit an, dass ein Entzündungswert im Intervall des jeweiligen Balkens liegt.
Während sich die Balken eines Histogramms mit absoluter Häufigkeit (Anzahl) zur Stichprobengröße aufaddieren, addieren sie sich beim Histogramm mit relativer Häufigkeit (Wahrscheinlichkeit) zu 1.
Die ersten Daten sind also eingetroffen, und Sie machen sich nun an die Auswertung. Das führt zu Sie zum Thema der heutigen Vorlesung: wie kann man Daten statistisch beschreiben?
Der Forschungsprozess
Lagemaße
Lagemaße
- Der weithin bekannte Durchschnittswert oder Mittelwert ist ein Beispiel für ein Lagemaß von Verteilungen.
- Man spricht dabei auch von der zentralen Tendenz (engl. central tendency) einer Verteilung
- Das Lagemaß ist neben dem Streumaß der wesentliche Parameter, um die Verteilung von Daten effizient (d.h. mit wenigen Parametern) zu beschreiben
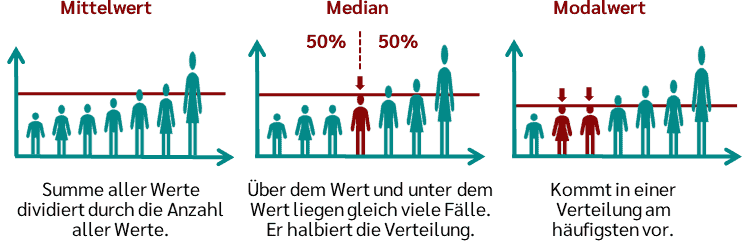
- Die drei wichtigsten Lagemaße sind:
- Mittelwert (gemeint ist das arithmetische Mittel)
- Median
- Modus (auch Modalwert)
Mittelwert
- Berechnung (verbal):
- Addiere alle \(n\) Stichprobenwerte
- Teile durch die Anzahl der Werte
- Berechnung (Formel):
\[ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i \]
- Notation: Strich über dem kleinen Letter der Zufallsvariable = Mittelwert der Zufallsvariable
Beispiel
Folgende Beobachtungen der Zufallsvariable \(X\) “Punktzahl in der Abi-Matheprüfung” werden in einer Stichprobe von 7 Psychologiestudierenden gemacht: \(\mathbf{x} = \{13, 7, 15, 8, 4, 9, 14\}\)
\[ \bar{x} = \frac{1}{7}(13+7+15+8+4+9+14) = = \frac{1}{7}\cdot 70 = 10 \]
Wann ist der Mittelwert sinnvoll?
- Der Mittelwert ist ein sinnvolles Lagemaß, wenn er nicht durch einzelne Ausreißer (extreme Werte) dominiert bzw. verzerrt wird.
| \(\mathbf{x}\) (z.B. Punktzahlen im Abi) | \(\bar{x}\) | Histogramm | Mittelwert sinnvoll? |
|---|---|---|---|
| \(\{13, 7, 15, 8, 4, 9, 14\}\) | \(10\) | 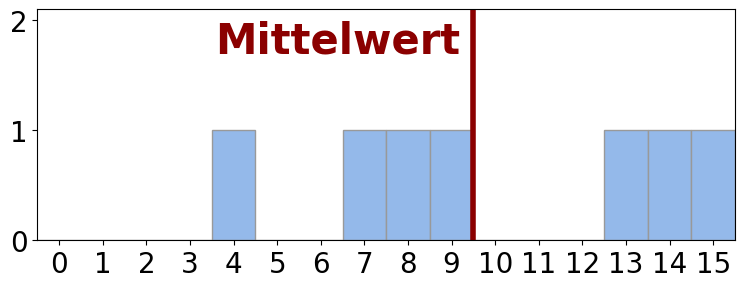 |
✓ |
| \(\{3, 1, 4, 2, 2, 6, 15\}\) | \(4.7\) | 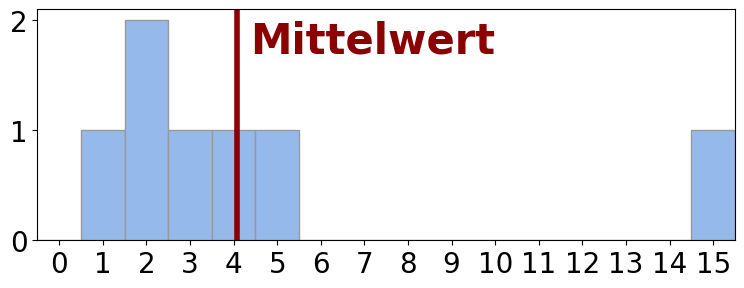 |
✗ |
| \(\{13, 15, 11, 12, 9, 14, 1\}\) | \(10.7\) | 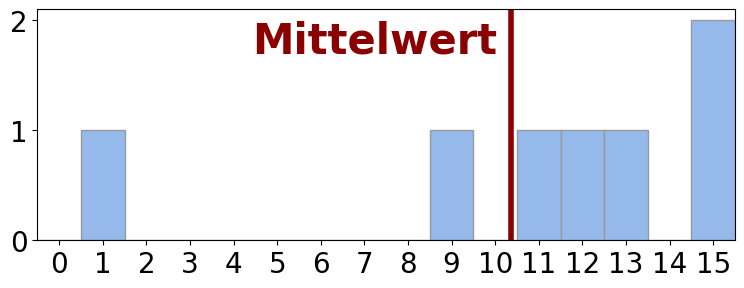 |
✗ |
Median
- Gibt es dominante Ausreißer in den Daten, so ist häufig der Median das sinnvollere Lagemaß
- Berechnung:
- Alle \(n\) Stichprobenwerte der Größe nach aufreihen
- Der Wert, der genau in der Mitte liegt, ist der Median
- Bei einer geraden Anzahl von Werten bilden zwei Werte die Mitte – in diesem Fall ist der Median der Mittelwert dieser beiden Werte
- \(\Big(\) Alternativ mit Formel: \(Tiefe_{\,\text{Median}}=\frac{n+1}{2}\Big)\)
- Der Median wird mit einer Tilde (~) über der Variablen bezeichnet: \(\tilde{x}, \tilde{y}, ..\)
Beispiel
Folgende Beobachtungen der Zufallsvariable \(X\) “Punktzahl in der Abi-Matheprüfung” werden in einer Stichprobe von 7 Psychologiestudierenden gemacht: \(\mathbf{x} = \{13, 7, 15, 8, 4, 9, 14\}\)
\[ \text{Sortierte Reihenfolge:} \;\mathbf{x} = \{4, 7, 8, \color{green}{\mathbf{9}}, 13, 14, 15\} \;\rightarrow\; \tilde{x} = 9 \]
Wir fügen den Wert eines weiteren Studierenden hinzu: \(\mathbf{x} = \{13, 7, 15, 8, 4, 9, 14, 10\}\)
\[ \text{Sortierte Reihenfolge:} \;\mathbf{x} = \{4, 7, 8, \color{green}{\mathbf{9}, \mathbf{10}}, 13, 14, 15\} \;\rightarrow\; \tilde{x} = \frac{9+10}{2} = 9.5 \]
Median
- Der Median ist außerdem sinnvoll bei:
- ordinalen Daten wie etwa diskreten Ratings (Skala von 1 bis 10), bei denen die Abstände zwischen Zahlen nicht interpretierbar sind.
- schiefen Verteilungen der Daten (dazu kommen wir noch)

- Der Median ist nicht sinnvoll, wenn:
- auch der Mittelwert ein sinnvolles Lagemaß darstellt (der Mittelwert hat einige hilfreiche mathematische Eigenschaften2).
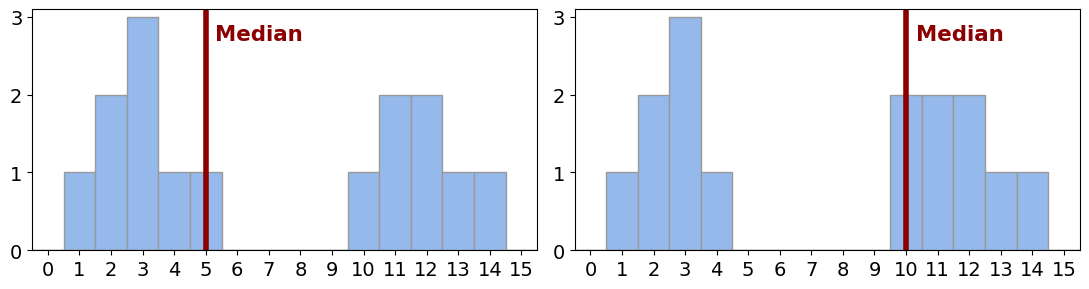
- in der zugrundeliegenden Verteilung zwei oder mehr Wertebereiche deutlich häufiger vorkommen als andere Wertebereiche, und diese Bereiche nicht überlappen (z.B. hat der Median von \(\{2, 2, 2, 2, 9, 9, 9\}\) den wenig aussagekräftigen Wert 2).
Modus
- In manchen Fällen ist es interessant zu wissen, was der häufigste Wert in einem Datensatz ist – dies ist der Modus.
- Berechnung:
- Zähle die Häufigkeit aller vorkommenden Werte
- Der häufigste Wert ist der Modus
- Im Fall von kategorialen Variablen ist der Modus das einzig mögliche Lagemaß (Beispiel: aus welchem Bundesland kommen die meisten von Ihnen?)
- Ein weiterer sinnvoller Anwendungsfall können schiefe Verteilungen sein:
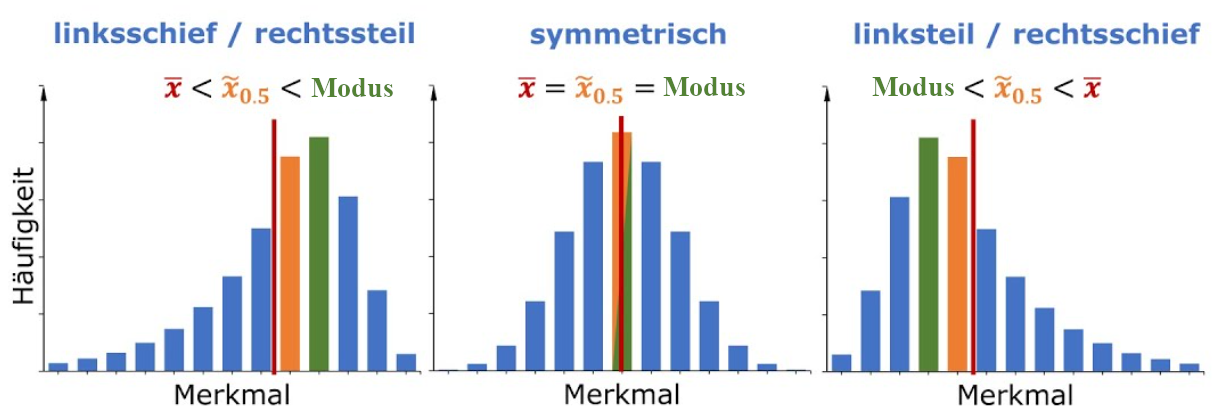
Streuungsmaße
Warum sind Streuungsmaße wichtig?
“In unserer Studie waren brünette Menschen im Schnitt 10 IQ-Punkte schlauer als blonde Menschen”
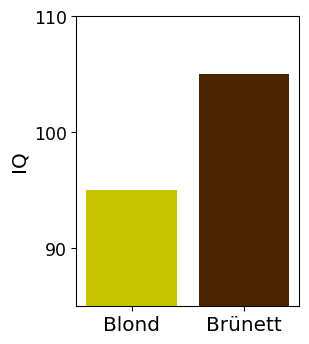
Behind the scenes:
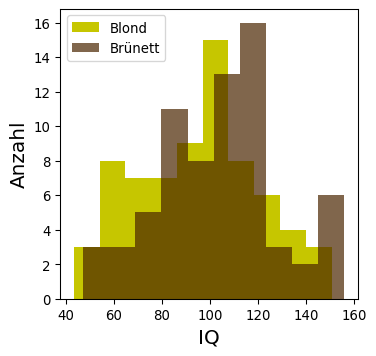
Warum sind Streuungsmaße wichtig?
 |
Wie schätzen Sie die Streuung / Variabilität folgender Verteilungen ein? |
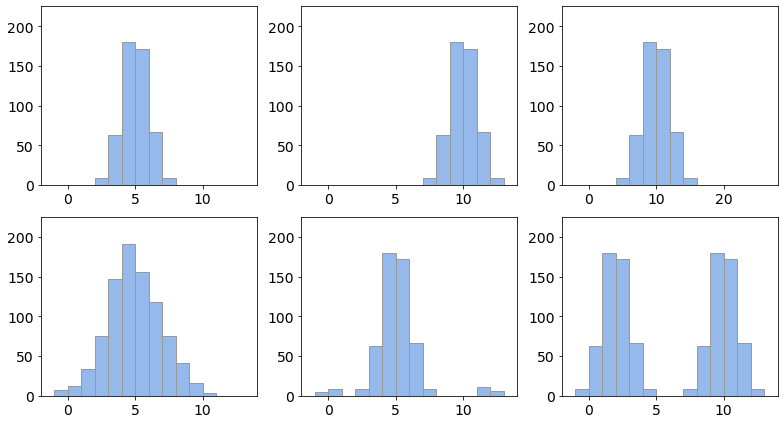
Streuungsmaße
- Streuungsmaße geben die Variabilität von Daten an
- Streuungsmaßes sind eine extrem wichtige Ergänzung zu Lagemaßen beim Bericht wissenschaftlicher Ergebnisse.
- Die Streuung von Daten kann ein Ausdruck echter Variabilität in der Stichprobe sein oder eine Folge der Messungenauigkeit (häufig beides).
- Je nach Skalenniveau und Zweck können verschiedene Streuungsmaße bestimmt werden:
- Spannweite (Range)
- Interquartilsabstand
- Varianz
- Standardabweichung
Spannweite / Range
- Die Spannweite oder Range ist die Differenz zwischen dem kleinsten und dem größten Wert:
\[ Range = x_{max} - x_{min} \]
- Einfachstes Streuungsmaß — sinnvoll, um dem Leser einen Eindruck der gesamten Spannbreite von Daten zu geben.
- Allerdings kaum Aussagekraft über die tatsächliche Variabilität der Daten
- Beispiel: die Spannbreite von \(\mathbf{x}=\{1, 10, 10, 10, 10, 10, 10, 10, 10, 10, 101\}\) ist \(101-1=100\), obwohl die Daten bis auf die zwei Ausreißer \(1\) und \(101\) keine Variabiltät aufweisen.

Range: Beispiele
Varianz
- Die Varianz ist definiert als die Summe der quadrierten Abweichungen aller Werte vom Mittelwert:
\[ Var(X) = \sigma^2 = \frac{1}{n}\sum_{i=1}^n\big(x_i-\bar{x}\big)^2 \]
(Die Varianz ist gleich der quadrierten Standardabweichung \(\sigma\) – letztere lernen wir noch kennen)
- Durch die Quadrierung wird verhindert, dass sich positive und negative Abweichungen gegenseitig aufheben.
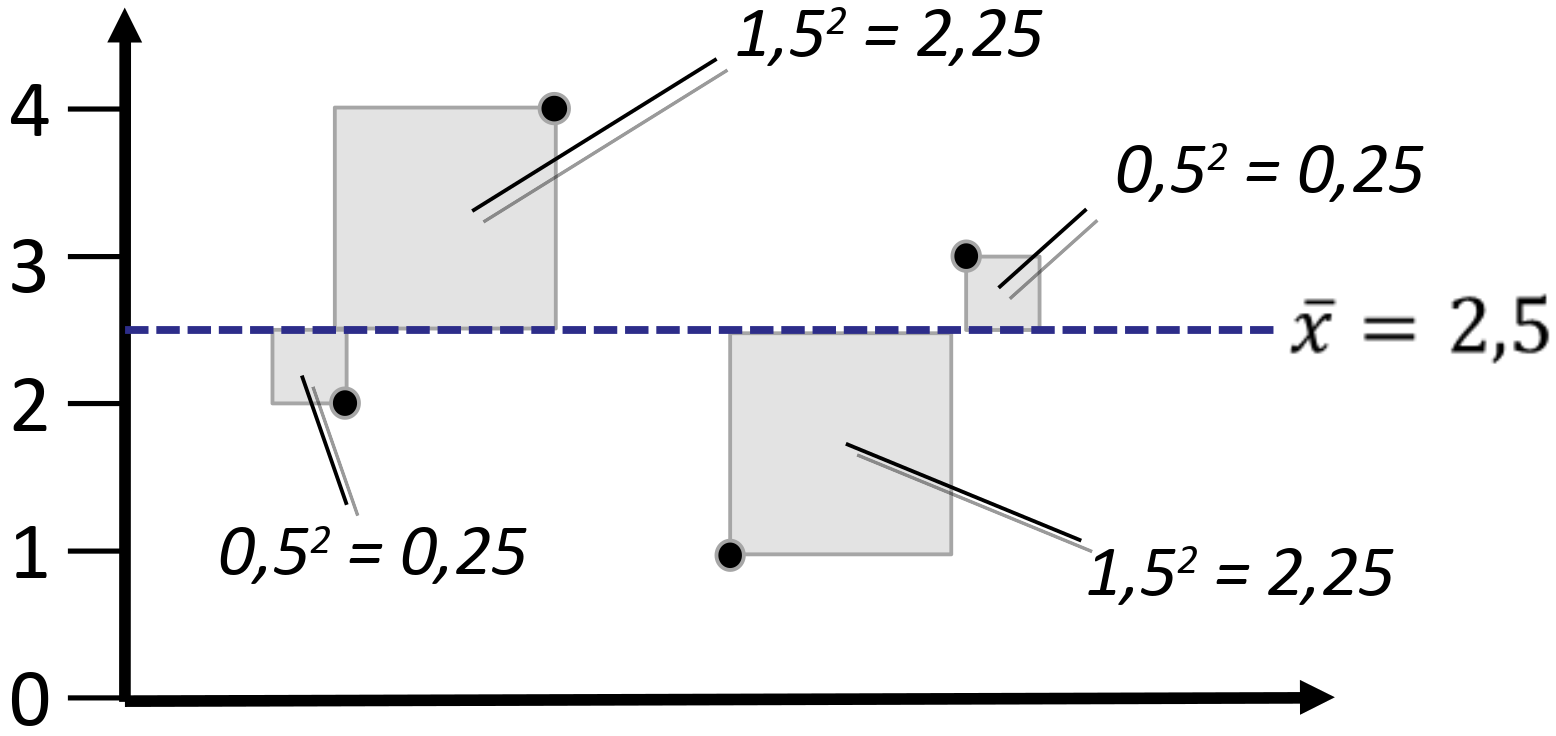
\[ \begin{aligned} \sigma^2 &= \frac{1}{4}\left(0{,}25+2{,}25+0{,}25+2{,}25\right) \\ &= \frac{1}{4}\cdot5=1{,}25 \end{aligned} \]
Warum werden werden nicht einfach die Absolutwerte der Differenzen genommen?

Prinzipiell wäre auch eine Formel für die Varianz mit Absolutabständen denkbar:
\[ Var_{\text{absolut}}(X) = \frac{1}{n}\sum_{i=1}^n\big|x_i-\bar{x}\big| \]
Über die Gründe, warum sich \(Var_{\text{absolut}}\) nicht durchgesetzt hat, streitet sich die Fachwelt. Neben historischen Gründen, gibt es aber einige Eigenschaften, die die Präferenz für Abstandsquadrate zumindest nachvollziehbar machen:
- Quadrierte Abstände gewichten Punkte, die weiter vom Mittelwert entfernt sind, höher. Dies entspricht einer “Bestrafung” von Ausreißern und kann ein wünschenswertes Verhalten sein.
- Analogie zur euklidischen Distanz (z.B. Satz des Pythagoras: \(a=\sqrt{b^2+c^2}\))
- Fortgeschritten: die Varianz mit Abstandsquadraten ist für alle \(x\) differenzierbar
(hingegen ist \(Var_{\text{absolut}}\) bei \(x=0\) nicht differenzierbar)
Weitergehende Literatur 5
Standardabweichung
- Ein Nachteil der Varianz ist, dass sie aufgrund der Abstandsquadrate in quadrierten Einheiten angegeben ist:

\(x=\{167\,cm, 181\,cm, 154\,cm, 192\,cm, 173\,cm\}\rightarrow Var(X)=180.4\,\color{red}{cm^2}\)
- Quadrierte Einheiten sind jedoch wenig intuitiv und schwer zu interpretieren.
- Aus diesem Grund wird häufig die Standardabweichung \(\sigma\) angegeben, welche die Wurzel der Varianz darstellt:
\[ \sigma=\sqrt{Var(X)}=\sqrt{\frac{1}{n}\sum_{i=1}^n\big(x_i-\bar{x}\big)^2} \]
- Die Standardabweichung drückt die Streuung in den Rohwerten der Skala aus.
- Sie wird häufig auch mit \(sd\) oder \(SD\) (für standard deviation) abgekürzt.
Einschub: Variablenbenennung
- In psychologischen Studien können in den allermeisten Fällen nur Stichproben getest werden und nicht die komplette Population.
- In der Statistik hat es sich eingebürgert, griechische Buchstaben für Kennwerte der Population und lateinische Buchstaben für Kennwerte der Stichprobe und zu verwenden.
- Das Zirkumflex (^) wird verwendet, wenn das Ziel ist, auf Basis eines Stichprobenkennwertes den analogen Kennwert in der Population zu schätzen.
| Stichprobe | Stichprobe (Schätzung für Population) | Population | |
|---|---|---|---|
| Mittelwert | \(\bar{x}\), \(m\), \(M\) | \(\hat{\mu}\) | \(\mu\) |
| Standardabweichung | \(s\) | \(\hat{\sigma}\) | \(\sigma\) |
| Varianz | \(s^2\) | \(\hat{\sigma}^2\) | \(\sigma^2\) |
| Korrelation | \(r\) | \(\hat{\rho}\) | \(\rho^2\) |
| Fallzahl | \(n\) | \(N\) |
- Wie wir noch sehen werden, gilt \(\bar{x}=\hat{\mu}\), aber (zumindest bei kleinen Stichproben) \(s\ne\hat{\sigma}\) bzw. \(s^2\ne\hat{\sigma}^2\).
Standardabweichung: Klassik-Beispiele
Interquartilsabstand (interquartile range = IQR)
- Quartile sind eine Spezialform von Quantilen
- Quantile teilen eine Verteilung von Daten in gleich große Abschnitte ein
- “gleich groß” = jeder Abschnitt hat gleich viele Datenpunkte
- Beispiel Dezile: Einteilung der Verteilung in 10 gleich große Abschnitte
- Hier: 20 Werte eingeteilt in 10 Abschnitte (Dezile) á 2 Werte
\[ \underbrace{1, 1,}_{\small{\text{1.Dezil}}}\;\underbrace{1, 2,}_{\small{\text{2.Dezil}}}\;2, 3, \;3, 5, \;5, 5, \;\color{white}{\underbrace{\color{black}{5, 6,}}_{\small{\color{black}{\text{...}}}}} \;6, 7, \;7, 7, \;7, 8, \;\underbrace{8, 8}_{\small{\text{10.Dezil}}} \]
- Beispiel Quintile: Einteilung der Verteilung in 5 gleich große Abschnitte
- Hier: 30 Werte eingeteilt in 5 Abschnitte (Quintile) á 6 Werte
\[ \underbrace{1, 1, 1, 1, 2, 2,}_{\small{\text{1.Quintil}}}\;\underbrace{2, 2, 2, 3, 3, 3,}_{\small{\text{2.Quintil}}}\;\underbrace{4, 4, 5, 5, 5, 5,}_{\small{\text{3.Quintil}}} \;\underbrace{5, 6, 6, 7, 7, 7,}_{\small{\text{4.Quintil}}} \;\underbrace{8, 8, 9, 9, 9, 9}_{\small{\text{5.Quintil}}} \]
- Beispiel Quartile: Einteilung der Verteilung in 4 gleich große Abschnitte
- Hier: 12 Werte in 4 Abschnitte (Quartile) á 3 Werte
\[ \underbrace{1, 1, 2,}_{\small{\text{1.Quartil}}}\;\underbrace{2, 2, 2,}_{\small{\text{2.Quartil}}}\;\underbrace{3, 4, 5,}_{\small{\text{3.Quartil}}} \;\underbrace{5, 6, 6}_{\small{\text{4.Quartil}}} \]
Interquartilsabstand (interquartile range = IQR)
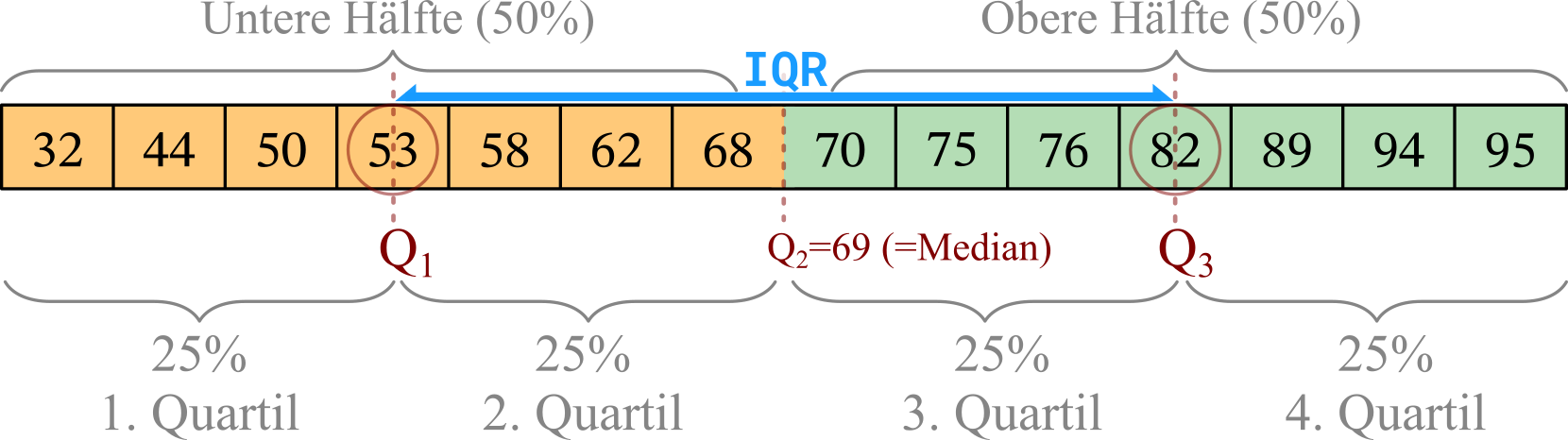
- Um eine Reihe von Daten in 4 gleich große Quartile zu teilen, sind genau drei Quartilsgrenzen notwendig
- Diese Quartilsgrenzen werden mit \(Q_1\), \(Q_2\), \(Q_3\) (bezogen auf Quartile) bzw. mit \(Q_{25\%}\), \(Q_{50\%}\), \(Q_{75\%}\) (bezogen auf Quantile) bezeichnet
- Der Interquartilsabstand (IQR) ist die Differenz aus der 75%-Quantilsgrenze und der 25%-Quantilsgrenze bzw. die Differenz aus der 3. und der 1. Quartilsgrenze:
\[ IQR = Q_{75\%} - Q_{25\%} = Q_3 - Q_1 \]
Interquartilsabstand (interquartile range = IQR)
- Berechnung des IQR:
- Sortiere alle Werte von klein nach groß
- Bestimme die Tiefe des Medians (runde ab bei unganzzahligem Wert):\(\,Tiefe_{\text{Median(abgerundet)}}\)
- Bestimme die Tiefe des Quartils: \(Tiefe_{\text{Quartil}}=\frac{Tiefe_{\text{Median(abgerundet)}}+1}{2}=\frac{\text{abgerundet}\big(\frac{n+1}{2}\big)+1}{2}\)
- Für das 25%-Quantil (\(Q_1\)) geht man von vorne in die Datenreihe
- Für das 75%-Quantil (\(Q_3\)) geht man von hinten in die Datenreihe
 |
Folgende 11 Werte werden beobachtet: \(x=\{1, 1, \color{darkred}{2}, \color{darkred}{3}, 3, \color{green}{3}, 4, \color{darkblue}{6}, \color{darkblue}{6}, 7, 9\}\) In diesem Fall ist der 6. Wert der Median, also \(\,\color{green}{Tiefe_{\text{Median(abgerundet)}}=6}\) Die Tiefe des Quartils ist damit \(Tiefe_{\text{Quartil}}=\frac{\color{darkgreen}{Tiefe_{\text{Median(abgerundet)}}}+1}{2}=\frac{6+1}{3}=3{,}5\) Der “\(3{,}5\)”-te Wert von vorne ist der Mittelwert aus \(\color{darkred}{2}\) und \(\color{darkred}{3}\) (\(\color{darkred}{Q_1=2{,}5}\)), der “\(3{,}5\)”-te Wert von hinten ist der Mittelwert aus \(\color{darkblue}{6}\) und \(\color{darkblue}{6}\) (\(\color{darkblue}{Q_3=6}\)) \(IQR = \color{darkblue}{Q_3} - \color{darkred}{Q_1} = \color{darkblue}{6} - \color{darkred}{2.5} = 3{,}5\) |
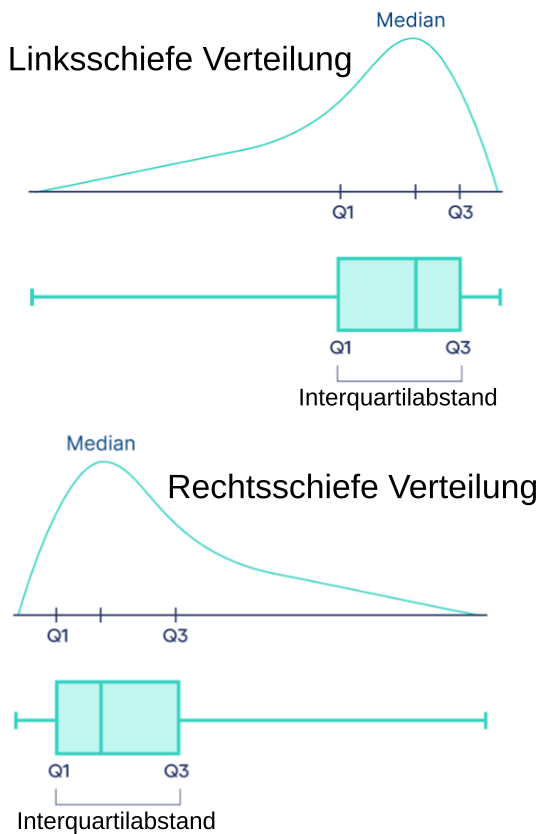
Wann ist der Interquartilsabstand ein sinnvolles Streuungsmaß?
Vereinfacht gesagt verhält sich der Interquartilsabstand zur Varianz, wie der Median zum Mittelwert zum Mittelwert.
- Die klassische Standardabweichung kann leicht durch einen einzelnen oder wenige extreme Datenpunkte verzerrt werden (insbesondere durch die Abstandsquadrierung).
- Der Interquartilsabstand ist robuster gegen Ausreißer, da er auf einem ähnlichen Prinzip wie der Median basiert: statt einem arithmetischen Mittel werden basiert der Wert auf tatsächlichen Datenpunkten in der Mitte der Verteilung.
- Wie dem Median ist es daher dem Interquartilsabstand “egal” ob etwa der höchste Wert 10 oder 10 Trillionen ist.
- Auch bei stark schiefen Verteilungen bietet sich der Interquartilsabstand an, da der von der Standardabweichung verwendete Bezugspunkt “Mittelwert” in diesem Fall problematisch ist.
Interquartilsabstand: Klassik-Beispiele
Die Streuungsmaße im Vergleich
| Spannbreite (Range) | ▪ Gibt die Ausdehnung des gesamten Wertebereiches an ▪ Auf kein bestimmtes Lagemaß bezogen ▪ Geringer statistischer Nutzen, manchmal interessante Zusatzinfo ▪ Maximal abhängig von Ausreißern |
| Varianz | ▪ Auf den Mittelwert bezogen (“wie stark streuen die Daten um den Mittelwert?”) ▪ Relativ anfällig gegenüber Ausreißern ▪ Unnatürliche quadrierte Einheiten |
| Standardabweichung | ▪ Wie Varianz, aber natürliche unquadrierte Einheiten |
| Interquartilsabstand | ▪ Auf kein bestimmtes Lagemaß bezogen ▪ Jedoch ähnliches Prinzip wie der Median und häufig im Zusammenhang mit diesem angegeben ▪ Robust gegenüber Ausreißern & sinnvoll bei schiefen Verteilungen |
Die Daten in Ihrer Beobachtungsstudie weisen keine größeren Ausreißer auf uns Sie entscheiden sich für Mittelwert bzw. Standardabweichung als Ihr Lage- bzw. Streuungsmaß. Für eine erste Kommunikation mit den anderen Task Forces erstellen Sie folgende Abbildung:

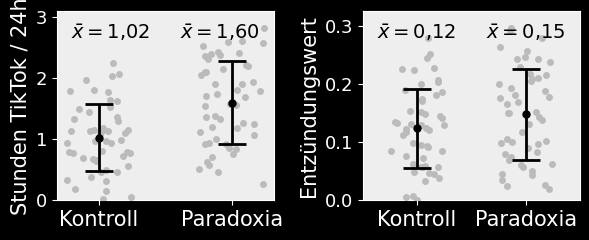

Aus den Werten und der Abbildung wird ersichtlich: tatsächlich sind auch die Entzündungswerte bei Paradoxikern erhöht! Auf Basis der Mittelwerte finden Sie also Evidenz für beide Hypothesen!

Vorlesung 03: Lage- und Streuungsmaße
Fußnoten
https://datatab.de/tutorial/mittelwert-median-modus
Beispielsweise ist der Mittelwert der Mittelwerte von zwei Gruppen mit je n Datenpunkten gleich dem Mittelwert aller 2*n Datenpunkte. Beim Median ist dies nicht gegeben. Auch beziehen sich viele statistische Standardtests auf den Mittelwert und nicht den Median.
https://youtu.be/inJ4OvU0zMA
https://www.shiksha.com/online-courses/articles/measures-of-dispersion-range-iqr-variance-standard-deviation/
https://web.archive.org/web/20221024193801/https://www4.hcmut.edu.vn/~ndlong/TK/mat/04_standard_deviation_vs_absolute_deviation.pdf